题目内容
（请给出正确答案）
[单选题]
设f（x，y)连续可偏导，且，下列条件中，可使得不等式f（x1，y1)＜f（x2，y2)成立的是（
A.x1＜x2，y1＜y2
B.x1＞x2，y1＞y2
C.x1＜x2，y1＞y2
D.x1＞x2，y1＜y2
查看答案
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
A.x1＜x2，y1＜y2
B.x1＞x2，y1＞y2
C.x1＜x2，y1＞y2
D.x1＞x2，y1＜y2
如果结果不匹配，请 联系老师 获取答案
更多“设f（x，y)连续可偏导，且，下列条件中，可使得不等式f（x…”相关的问题
设函数f(x)在区间[0，1]上连续，在(0，1)内可导，且满足条件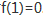
试证：存在ξ∈(0，1)，使f(ξ)+ξf'(ξ)=0
设z=f(2x-y)+g(x，xy)，其中f(x)二阶可导，g(u，v)具有连续的二阶偏导数，问
设函数f(x)，F(x)在[a，b]上连续，在(a，b)内可导，且F'(x)≠0，x∈(a，b)．由于f(x)，F(x)在[a，b]上都满足拉格朗日中值定理的条件，故存在点ξ∈(a，b)，使
f(b)-f(a)=f'(ξ)(b-a)， (1)
F(b)-F(a)=F'(ξ)(b-a)， (2)
又，F'(x)≠0，x∈(a，b)，(1)，(2)两式相除，即有
以上证明柯西中值定理的方法对吗？
计算下列各题:
(1)设F(u,v)有连续偏导数,方程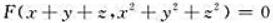
确定函数z=f(x,y),求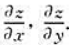
(2)设u=f(x,y,z)有连续偏导数,y=y(x)和z=z(x)分别由方程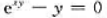
和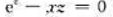
所确定,求du/dx.
z=f(x，y)的偏导数
设f(x)二阶连续可导，且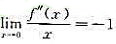
，则()。
A.f(0)是f(x)的极小值
B.f(0)是f(x)的极大值
C.(0，f(0))是曲线y=f(x)的拐点
D.x=0是f(x)的驻点但不是极值点
设f(x)具有二阶连续导数，且f(0)=0，试证：
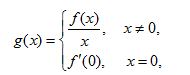
可导，且导函数连续.
设函数f(x)在闭区间[a，b]上连续，在开区间(a，b)内可导，且f'(x)＞0，极限limx→a+f(2x？a)x？a存在，证明：
①在(a，b)内f(x)＞0
②在(a，b)内存在点ξ，使b2？a2∫baf(x)dx＝2ξf(ξ)
③在(a，b)中存在与②中ξ相异的η，使f′（η）（b2-a2）=2ξξ？a∫baf(x)dx．
求a，b何值时，f(x)在x=0处连续且可导
